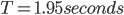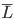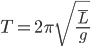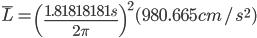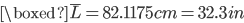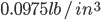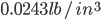I needed approximately 30 BF of walnut. I checked all of the local stores, and found the availability of walnut in the quantities I needed was fairly limited. One store wanted $15/BF, however $8-10/BF seemed to be closer. It wasn't terribly eager to spend $450 on wood. The only available boards were < 10", therefore, I was going to have to glue up panels for the sides.
I scoured Craigslist, and even went to a garage sale that had 300-400 BF. However, the boards were a bit too rough for my comfort level, almost all with live edges. Again, getting wide enough and long enough boards was going to be a challenge.
I found a very assuming Craigslist post of someone trying to sell Walnut. We exchanged a few emails, but I wasn't overly optimistic. I borrowed the neighbors truck, and headed to his property. It was nestled in the woods, with piles of wood and logs everywhere. It was run by two gentlemen. As soon as I got there, they had 6 boards, 5/4+ that were 9 3/4" wide and over 14' long. It was exactly what I was looking for! They had milled it that morning. The wood itself has a beautiful grain pattern. We did some quick math based on assumed yields (6 boards @ 12', 9" width, 1" thick). Approximately 50 BF, he wanted $5/BF. We agreed on $200.
We went to load them in to the truck, and quickly discovered that was going to be a disaster. Fourteen feet boards just don't fit in a pickup. They offered to throw it on their trailer and drop it off at my house. Very generous and convenient.
 I also mentioned that I would love to get a 15"x15" piece to use for the clockface. We walked around his yard, looking at various logs, and seeing if we could find something large enough. We located a good looking burl that had good potential. They tossed in on the mill and started slicing it up. Unfortunately, there was a bit of rot on the inside, and a 15"x15" piece just wasn't in the cards. They were confident they would find something that would work and let me know.
I also mentioned that I would love to get a 15"x15" piece to use for the clockface. We walked around his yard, looking at various logs, and seeing if we could find something large enough. We located a good looking burl that had good potential. They tossed in on the mill and started slicing it up. Unfortunately, there was a bit of rot on the inside, and a 15"x15" piece just wasn't in the cards. They were confident they would find something that would work and let me know.
 The wood made it home without any issue. I now have it stickered and end sealed with polyeurethane. The tough part is now going to be waiting for it to reach the proper moisture content. It currently is in the 25-35% range. I believe 12% is a reasonable target.
The wood made it home without any issue. I now have it stickered and end sealed with polyeurethane. The tough part is now going to be waiting for it to reach the proper moisture content. It currently is in the 25-35% range. I believe 12% is a reasonable target.
I did a quick recalc on the total volume. 14.5' x 9 3/4" x 8" (total thickness) = 94 BF! That works out to $2.13/BF! It is hard to complain about that.
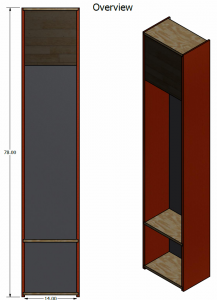
 Also, since the boards are 9 3/4" wide, I believe I can make the sides without gluing two together. A 9" depth should work great. Since they are 14.5' long, I can use a single board to make both sides, and another board to make the back. Figure another board for the rest, and suddenly I have twice as much wood as I need. My original figures (8 boards) were based on requiring glueups and 8' lengths. I really scored on this one. And I know I'll be back to visit these gentleman.
Also, since the boards are 9 3/4" wide, I believe I can make the sides without gluing two together. A 9" depth should work great. Since they are 14.5' long, I can use a single board to make both sides, and another board to make the back. Figure another board for the rest, and suddenly I have twice as much wood as I need. My original figures (8 boards) were based on requiring glueups and 8' lengths. I really scored on this one. And I know I'll be back to visit these gentleman.
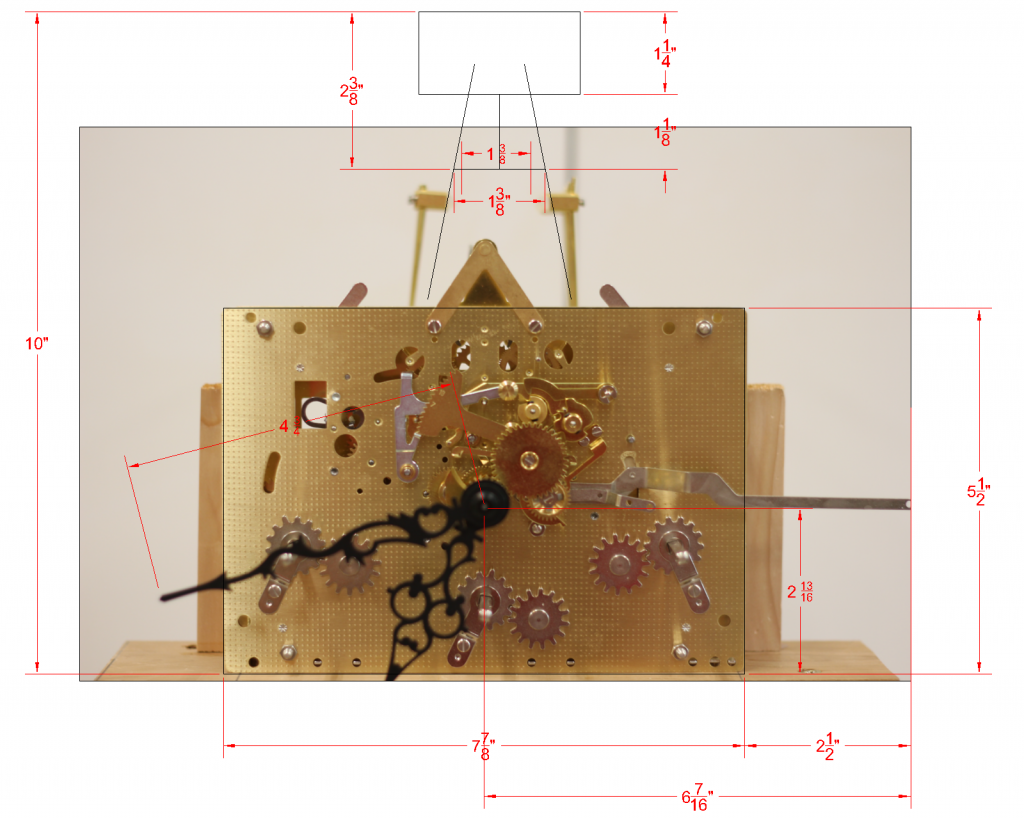

 I finally got tired of having a movement, and not having it in action. However, a reasonable case is way to far away, so I put together a test rig. The rig consisted of some 2x4s, and a cedar top plate that allowed the cables for the weights to pass through. I picked up some lead shot (for making shot gun shells) for weight. The left two weights are 7.7 lb mason jars. The right weight is a 9.9 growler. The horizontal bar was required to keep the weights from interfering with the pendulum.
I finally got tired of having a movement, and not having it in action. However, a reasonable case is way to far away, so I put together a test rig. The rig consisted of some 2x4s, and a cedar top plate that allowed the cables for the weights to pass through. I picked up some lead shot (for making shot gun shells) for weight. The left two weights are 7.7 lb mason jars. The right weight is a 9.9 growler. The horizontal bar was required to keep the weights from interfering with the pendulum.