The pendulum is the most important parameter in keeping accurate time.  Therefore, it is critical to get the pendulum design correct.

The Period

The only parameter governing the period of an ideal pendulum (on earth), is the length.

The 1161-853/94 is geared for 3960 beats per hour [Hermle Service Manual].  In order to make the math work out correctly, I presume that each half-cycle of the pendulum is a beat.

$f = \frac{3960 beats}{hour} \cdot \frac{1 hour}{3600 seconds} = 1.1 \frac{beats}{second}$

$f = 1.1 \frac{beats}{second} \cdot \frac{1 cycle}{2 beats} = 0.55 Hz$

$T = \frac{1}{f} = \frac{1}{0.55Hz}$

$\boxed{T = 1.\overline{81} seconds}$

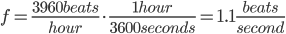
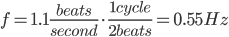
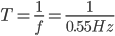
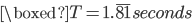
Therefore, we are going to have to target a pendulum design that maintains a $1.8181 second$ period.

Let's see how that compares with an ideal 94cm pendulum.

$T \approx 2 \pi \sqrt{\frac{L}{g}} = 2 \pi \sqrt{\frac{94 cm}{981 cm/s^2}}$

$T = 1.95 seconds$

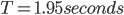
Well, it looks like an ideal pendulum isn't going to do the trick at 94 cm.  Therefore, what we really want is a pendulum with an effective length, 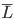$\bar{L}$, of

$T = 2 \pi \sqrt{\frac{\bar{L}}{g}}$

$\bar{L} = \left( \frac{T}{2 \pi} \right)^2 g$

$\bar{L} = \left( \frac{1.81818181s}{2 \pi} \right)^2 (980.665 cm/s^2)$

$\boxed{\bar{L} = 82.1175 cm = 32.3 in}$

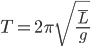
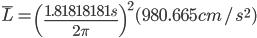
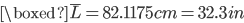
Therefore, what we really want, is a pendulum with an effective length of 32.3 in!

Physical Design

The pendulum will consist of two components.  See the Introduction for the inspiration for this design.

Bob

A bit arbitrarily, the bob was selected to be a 4" diameter, 1" thick, 6061 aluminum disc.  Assuming a density of 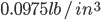$0.0975 lb/in^3$, the bob will weight 1.23 lb.

Rod

The rod will consist of a 3/8" x 3/8" x 1/16" U-Shaped 6061 aluminum channel with a walnut inlay.  Using the same assumed density of aluminum, and a density of walnut of 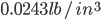$0.0243 lb/in^3$, the rod will weigh 0.012lb.

Length

I have to admit, I put together a fairly comprehensive spreadsheet to calculate the effective length and period.  I attempted to account for the moment of inertia of the rod and the bob itself.  However, at the end of the day, the eccentricity of the bob outweighs the other factors.  Therefore, the distance to the center of the bob should be 32.3 in.

Connection to Movement

The movement has a pendulum leader that is 5.5" long (should be included in the total pendulum length.  There are hooks available that are designed to interface with the pendulum that I will likely use. However, I still need to develop a way to tweak the length.